- English
- Français
- Nederlands
Table of Contents
Urbicande en 1°S
by Nathalie Aymé - La Réunion
1 - Introduction
 Connaissez-vous cette bande dessinée d'une qualité exceptionnelle, tant du point de vue du dessin qu'au niveau de son contenu? Celle-ci évoque un phénomène mystérieux dont on peut simuler l'évolution sur Cabri.
Connaissez-vous cette bande dessinée d'une qualité exceptionnelle, tant du point de vue du dessin qu'au niveau de son contenu? Celle-ci évoque un phénomène mystérieux dont on peut simuler l'évolution sur Cabri.
Il s'agit de La fièvre d'Urbicande de Peeters et Schuiten, aux Editions Casterman.
Les thèmes mathématiques abordés dans cette BD sont du niveau de la classe de première scientifique. Elle permet de parler de perspective cavalière, de tenter de modéliser un phénomène physique très curieux à l'aide de suites numériques, cette modélisation faisant appel à des notions variées de 1èreS : factorisation d'un polynôme du troisième degré, programmation d'une suite sur calculatrice…
Présentation générale
De quoi s'agit-il ? Quel est ce phénomène mystérieux dont je vous parle qui ferait un superbe TP de première S ? En deux mots : un cube, constitué d'une matière organique “auto-génératrice” a l'extraordinaire faculté de croître et de se multiplier !

Dans une ville d'une autre galaxie - ou d'un univers parallèle - nommée Urbicande, un cube très mystérieux est découvert au cours de fouilles et déposé sur le bureau d'Eugen Robick, l'urbatecte concepteur de la ville. Ce dernier, très intrigué par ce cube, ne cesse de l'observer et réalise le premier que ce cube possède une activité organique. En effet, les arêtes du cube se mettent à pousser, en même temps qu'elles se mettent à grandir !
Ainsi, sur chaque face du cube initial vient se greffer un nouveau cube pour constituer le réseau de première génération, puis sur chaque face de libre du réseau de première génération, se crée un autre cube pour élaborer le réseau de seconde génération et ainsi de suite jusqu'à ce que la ville soit entièrement recouverte par ce réseau venu d'ailleurs.

Mais je ne saurai vous décrire le phénomène aussi bien que La fièvre d'Urbicande elle-même que je vous conseille de lire sans plus tarder. Vous pouvez aussi visiter le site vers lequel les liens de cette page renvoient.
Tout au long de votre lecture, vous découvrirez vous-même le phénomène, extrêmement bien décrit par Eugen Robick, notre héros, architecte (“urbatecte” dans la BD) qui suit de près son évolution.
Eugen Robick, réellement époustouflé par la nature de ce phénomène tente de le mettre en équation et vous pourrez admirer à loisir les brouillons qu'il noircit tout au long de ses calculs.

J'ai pu savourer la lecture de cette BD en prenant un papier, un crayon et en vérifiant les calculs de notre héros.
Les calculs s'avéraient être fondés…
Quelle aubaine! J'avais une première S au lycée Evariste de Parny (Ile de la Réunion), et je me suis réjouie à l'idée de leur préparer un “devoir maison” un peu plus original que d'habitude.
J'avais envie de créer un devoir qui passionnerait tout le monde, qui leur donnerait envie de chercher, même si c'était un peu difficile. Et là, j'avais le moyen de le faire. Les élèves ont eu à faire ce devoir un peu gourmand en investissement personnel pendant les vacances de l'été austral (la période cyclonique de l'hémisphère sud nous vaut un mois et demi de vacances en janvier-février). Je vous propose donc, dans un premier temps, le sujet que j'ai écrit pour mes élèves et dans un deuxième temps, les figures CABRI réalisées pour simuler l'évolution du phénomène. On pourra donc les utiliser, au choix, lors de la présentation du devoir, ou lors de la correction. Leur réalisation étant assez longue, vous ne pourrez (éventuellement) les élaborer avec des élèves qu'au cours d'une activité de type club. Ces figures ont été complétées par des réalisations “opaques” pour la mise en ligne de ces pages, par le webmestre d'abraCAdaBRI.
Commentaires sur l'activité
C'est une formidable aventure que j'ai ainsi vécue avec mes élèves autour de La fièvre d'Urbicande. Cette activité nous a permis de nous investir à fond dans un sujet rendu passionnant par son contexte inusuel et attractif. Je dis bien nous, car travailler sur une telle activité ne se fait pas en une aprés-midi, tant pour les élèves que leur enseignant. Mais le jeu en vaut la chandelle : ce n'est pas du temps perdu compte tenu des notions mathématiques abordées lorsque l'on veut étudier ce phénomène.
Les élèves se sont réellement investis dans le travail demandé. Ils ont manipulé des calculs sur les suites comme je ne les avais jamais vu le faire en classe. Leur imagination fertile a permis (voir le texte du devoir) de baptiser le réseau de seconde génération de plusieurs noms : génération cuboctaèdre, cubicandoctaèdrienne, le réseau de Robick, le Robick-cube, l'octaréseau …
Certains ont dessiné des réseaux de secondes générations magnifiques, même s'ils ont avoué y avoir planché un certain temps. En fait, j'ai été en extase devant leurs devoirs.
J'espère vous faire partager, à travers les pages suivantes, un peu de mon enthousiasme ressenti en menant cette activité. Laissez vous projeter sur Urbicande pendant quelques semaines avec vos élèves, vous ne le regretterez pas. Côté pratique, vous pouvez par exemple faire commander une dizaine de BD par votre CDI en persuadant votre documentaliste de l'intérêt majeur de cet achat pour enrichir la bibliothèque mathématique de votre lycée.
Nathalie Aymé
2 - Le devoir de maths
Rappelons que ce devoir a été donné pendant les grandes vacances qui, à La Réunion, sont … au milieu de l'année scolaire, période cyclonique “oblige”. Il est clair que le texte a été adapté au format HTML et agrémenté d'images prises sur le site d'Urbicande. Une solution est disponible en téléchargement en fin de page.
Maths et Bande Dessinée
Lecture mathématique de la bande dessinée
de Schuitten et Peeters “La fièvre d'Urbicande”
 Urbicande est une ville d'une autre planète située dans une autre galaxie, à des millions d'années-lumière de la nôtre … Urbicande est très belle, très structurée, avec de grands monuments d'une rare beauté architecturale. Larges avenues, façades harmonieuses, jardins majestueux … tout ceci reflète une ville puissante dont le développement urbain a été l'oeuvre quasi-totale de l'urbatecte Eugen Robick.
Urbicande est une ville d'une autre planète située dans une autre galaxie, à des millions d'années-lumière de la nôtre … Urbicande est très belle, très structurée, avec de grands monuments d'une rare beauté architecturale. Larges avenues, façades harmonieuses, jardins majestueux … tout ceci reflète une ville puissante dont le développement urbain a été l'oeuvre quasi-totale de l'urbatecte Eugen Robick.
Un cube mystérieux a été déposé sur le bureau d'Eugen Robick. Ce cube est à l'origine du développement d'un phénomène jamais vu jusqu'alors. L'urbatecte étudie de très près l'évolution de ce phénomène, car la ville est menacée.
A - Lecture dirigée des extraits de la bande dessinée
Relever, page par page, toutes les informations concernant l'évolution du phénomène : date / heure, dimension des arêtes du cube, nombre de cubes, etc.
Relever toutes ces informations dans un tableau du type :
| n° de la page | Date | Info. de type descriptif | Info. de type quantitatif |
|---|---|---|---|
| — | — | — | — |
On essaiera notamment de comprendre les brouillons de l'urbatecte Robick. Que représente un ?
B - Prévision du phénomène. Mise en équation
Robick expose l'évolution du phénomène devant l'Assemblée de la ville lors d'une réunion exceptionnelle.
| Cube initial: u0 = 1 | 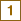 | Réseau de première génération: u1 = 7 |  |
Coupe suivant un plan de symétrie du réseau
a. À partir des schémas observés sur les brouillons de l'urbatecte, dessiner une coupe des réseaux de seconde et troisième génération. En déduire u2 et u3.
b. Montrer alors que sa formule donant un en fonction de n, exposée devant l'Académie est juste. Pour cela, utiliser les relations (déjà démontrées par ailleurs) :
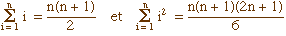
En déduire que un est un polynôme de degré 3 en n, que l'on factorisera.
c. Remplir alors le tableau suivant :
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Un | — | — | — | — | — | — | — | — | — | — | — |
Répondre à l'invitation de Robick à l'Assemblée générale (page 47) : “Je vous laisse imaginer ce que seront u20, u30, u50 …”.
C - Un peu de schémas dans l'espace
a. Dessiner dans l'espace le réseau de première génération, en n'indiquant que les traits des arêtes visibles.
b. En reliant les milieux des arêtes des cubes externes d'un réseau donné, on matérialise un solide qui englobe presque complètement le réseau. On peut considérer que le volume de ce solide est une bonne approximation du volume du réseau. La coupe par un plan de symétrie du réseau montre que la section de ce solide est un carré. Dessiner ce solide en perspective calière. Combien de face a-t-il ? d'arêtes ? de sommets ? quel est son nom ? Inventer alors un nom à ce réseau construit autour du cube initial, à la génération n.
D - Evolution des arêtes du cube
Par un phénomène inattendu, la progression s'est arrêtée brusquement dès que le réseau a recouvert l'ensemble de la ville d'Urbicande. On cherche à répondre à la question suivante :
En supposant qu'Urbicande soit une ville dont la base est un cercle de 10 km de diamètre, et en supposant que le bureau d'Eugen Robick soit situé en plein centre-ville, à quelle génération la progression a-t-elle stoppé ?
a. On envisage dans cette question que l'arête a0 du cube initial ne varie pas pendant le phénomène.
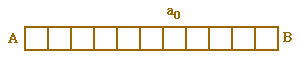
Combien y-a-t-il de cubes sur la diagonale [AC] du réseau à lanième génération ?
En recherchant a0 parmi les données quantitatives fournies par Robick, en déduire la réponse à la question posée.
b. En fait il faut beaucoup moins de générations. On peut en effet imaginer, d'après les descriptions de l'urbatecte, que l'arête du cube initial suit une progression géométrique. On trouve en effet (page 47), cette remarque de Robick devant l'Assemblée :
“Si la progression se poursuit au même rythme, chacune des arêtes sera à ce moment longue de plusieurs mètres”
En notant toujours a0 l'arête du cube initial, et a1 celle des cubes de la première génération, on peut estimer, d'après un brouillon de Robick que a1 est environ 20 cm. Donner la raison de cette progression - supposée géométrique - sous forme fractionnaire, et l'expression de la longueur an de l'arête des cubes à lanième génération, en fonction de a0 et de n.
Montrer alors que la question posée revient à chercher à partir de quel rang n0 on a l'inégalité :
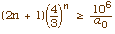
En programmant sur votre calculatrice la suite de terme général wn = (2n + 1)(4/3)n, donner la valeur de n0 qui convient.
c. Donner le volume total Vn du réseau à la génération n en fonction de un, le nombre de cubes du réseau et de l'arête an, à la nième génération. En déduire ce volume pour n = n0, l'exprimer en km3.
Quel est le volume du solide approchant le réseau comme étudié dans la partie C, lorsque n= n0 ? Le comparer au volume du réseau Vn0.
Charger une solution du devoir dans un des trois formats au choix :
3 - Figure Cabri 2 D
Dans cette page, on se propose de faire une figure Cabri qui compte les cubes suivant les générations successives dans une simulation 2D du phénomène (Partie B du devoir).
La figure finale
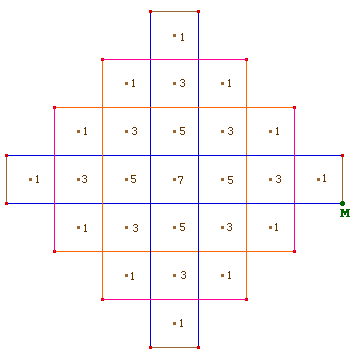
Cette figure Cabri va vous permettre de simuler la croissance du Réseau dans un de ses plans de symétrie, l'intérêt principal étant de voir les générations de cubes se former et d'aider les élèves à compter les cubes superposés au centre de chaque carré. Vous imaginez donc que, à une génération donnée, vous applatissez le réseau entier sur un plan de symétrie du réseau. Nous allons simuler cette projection jusqu'à la troisième génération.
Lancer la figure urbien2d.fig
Voir plutôt une animation gif de la figure 2D:
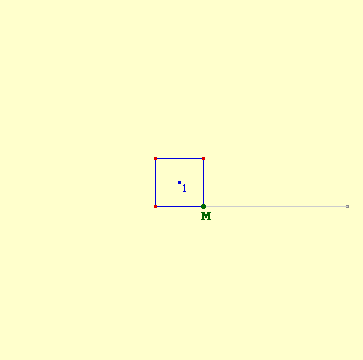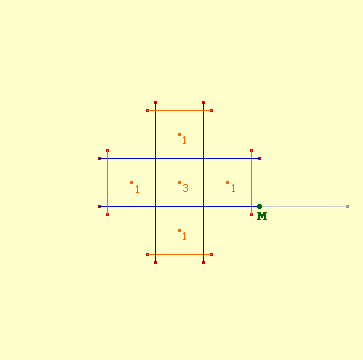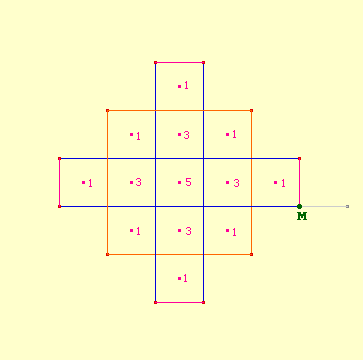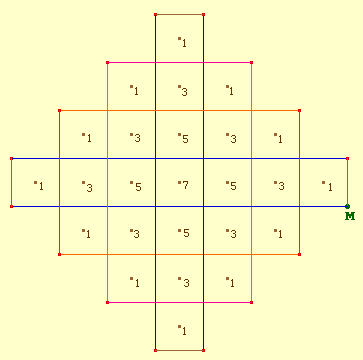
Illustration des autres générations
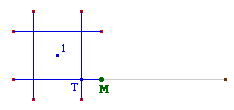
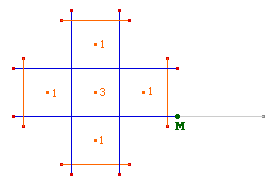
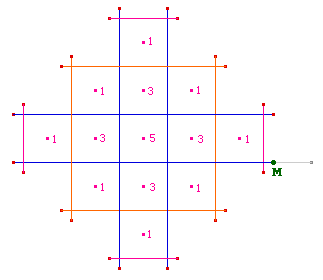
Indications sur les aspects logiques de la construction
La construction des segments formant les projections des arêtes ne pose pas de problèmes particuliers. Il est néanmoins intéressant d'optimiser les constructions. Cela a été décrit en détail dans le numéro 6 de la revue papier d'abraCAdaBI.
Il est plus intéressant de s'attarder sur la construction du comptage des cubes empilés lors de la projection plane. Les nombres croissent naturellement de 2 à chaque génération. Il faut donc construire des points qui n'existent que quand la situation est dans une génération donnée, ce qui correspond, pour le point M mobile, à l'appartenance à un segment semi-ouvert de type [AB[ puisqu'en B on est à la génération suivante.
On est donc en pleine géométrie logique. Cette macro Intérieur segment ouvert a déjà été traitée dans l'exercice 1 de la page de complément à l'introduction aux macros de base d'Alice.
Pour un point ainsi construit sous M, on construit sur le centre des carrés, un point logique, par la macro Ping-Pong (appelée dans l'article Existence Conditionnelle) dont la présentation a été faite à cette page. En pratique on le fait une seule fois pour chaque nombre, le reste se complète par les symétries du carré de la génération 0. C'est ce point logique qui reçoit comme nom le nombre de cubes projetés à cet endroit dans la génération en cours.
Pour la génération 3, il faut traiter le cas du point à l'extrémité du segment. Cela se fait simplement en construisant un segment un peu plus long (comme pour la génération 4) et en testant l'appartenance du point M à ce dernier segment par la macro Intérieur Segment traitée à cette page : c'est ainsi une façon de tester s'il est à l'extrémité du segment précédent qu'il doit parcourir.
Plus techniquement, si M parcourt un segment [AB], pour tester s'il est en B, on peut construire C le symétrique de A par rapport à B. M est en B s'il appartient au segment [BC].
4 - Figures Cabri 3 D
Dans cette page, on trouvera deux simulations de la construction Cabri du phénomène étudié par Eugène Robick telles qu'elles ont été effectuées par les élèves en activités de Club autour du thème d'Urbicande (Partie C du devoir).
Une première figure
Cette figure Cabri permet de simuler la croissance du Réseau en perspective cavalière
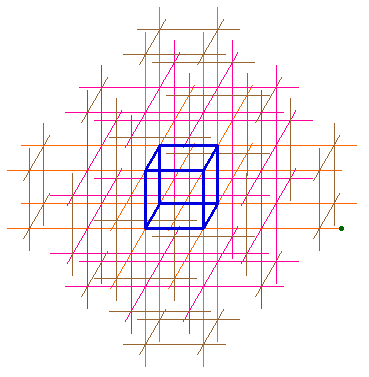
Lancer la figure Urbi3Da.fig en 3D
Les utilisateurs ne disposant pas de Cabri II peuvent consulter une animation gif rapide ou plus soignée .
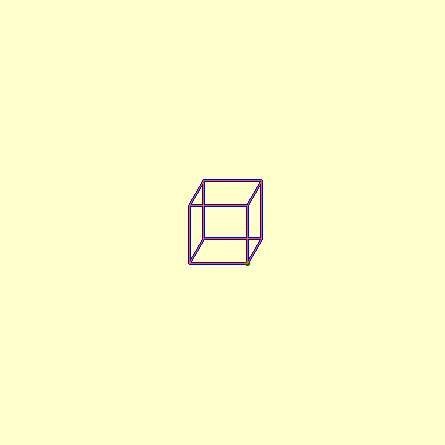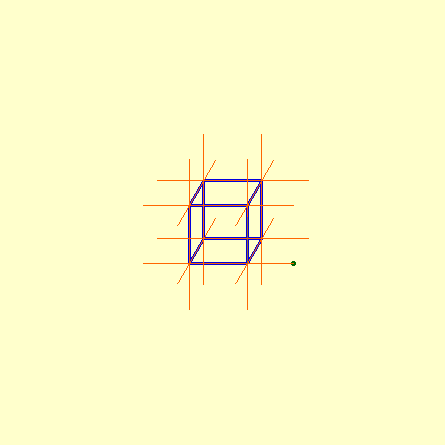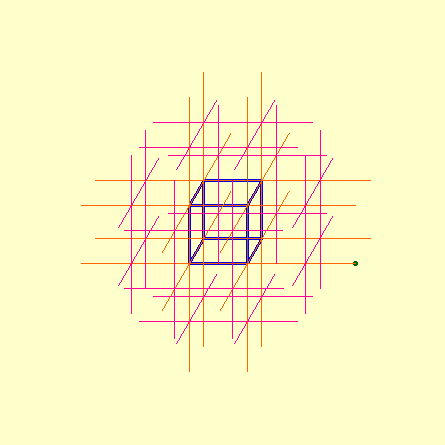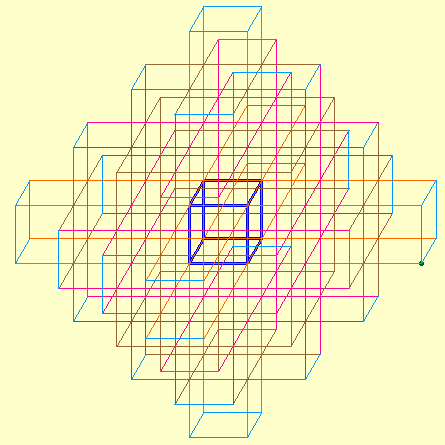
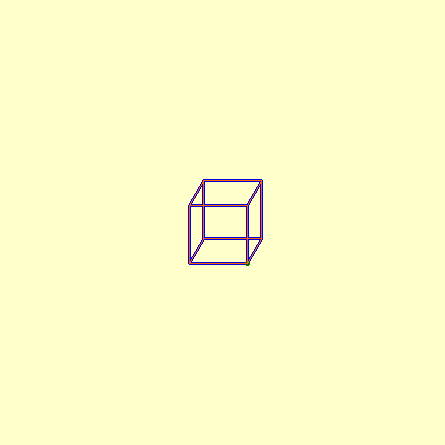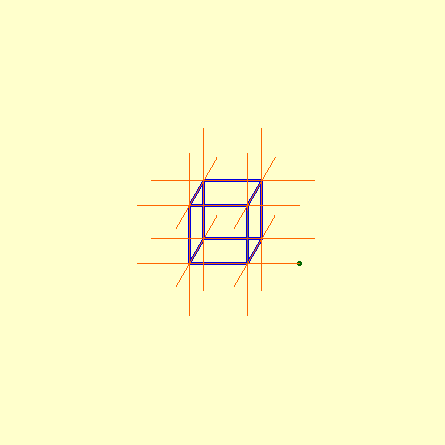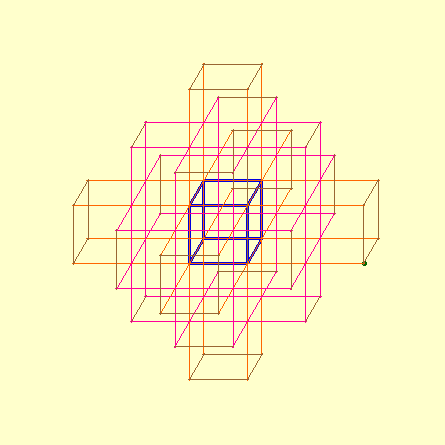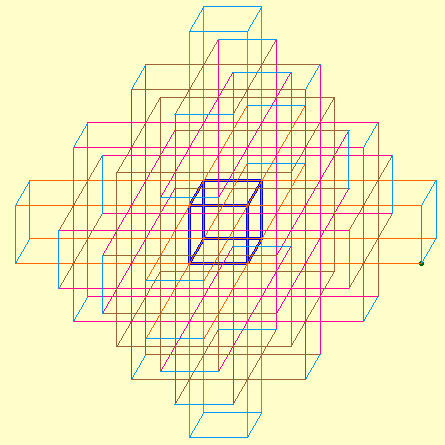
Illustration des autres générations
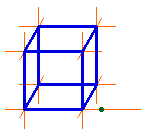
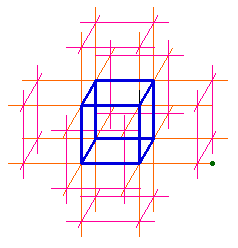
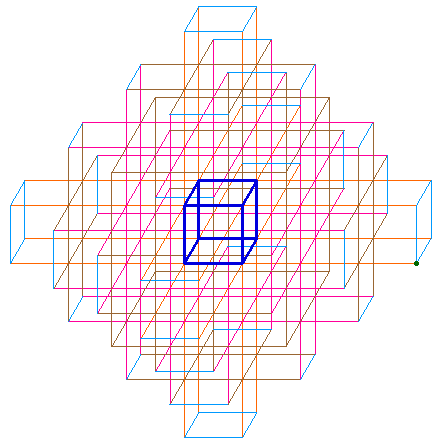
Une seconde figure
Cette autre figure Cabri simule la croissance par saut, avec diminution de la taille à l'écran quand M s'éloigne :
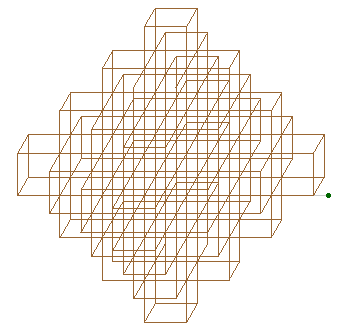

Lancer la figure Urbi3Db.fig en 3D.
Illustration des autres générations
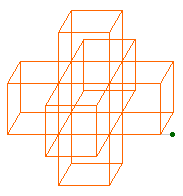
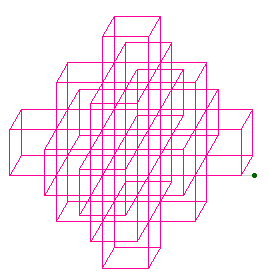
Le principe de construction de ces figures - et surtout leur optimisation - a été décrit en détail dans le numéro 7 d'abraCAdaBRI.
5 - Copies d'élèves
Les devoirs ont été traités avec une minutie toute particulière, accompagnés de nombreux schémas. Voici deux extraits de copies d'élèves.
Extrait de la partie A
Il s'agissait de chercher tous les indices dans les 17 pages de la BD données aux élèves pour faire le devoir. Cette page permet concrètement de voir les informations sur lesquelles travaillaient les élèves.
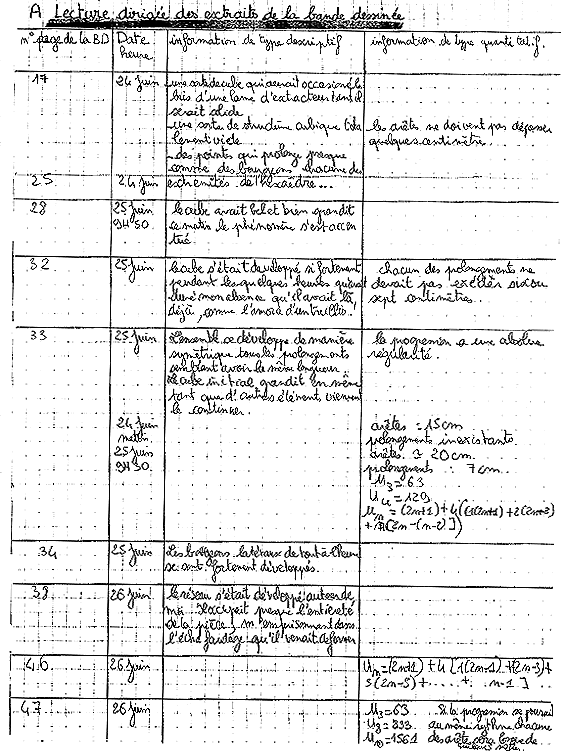
Extrait de la partie B
Il s'agissait de déterminer le nombre de cubes. Dans sa dernière phrase l'élève note une erreur de la BD. En fait il a lu un “n-1” alors qu'il était écrit un “n.1”.
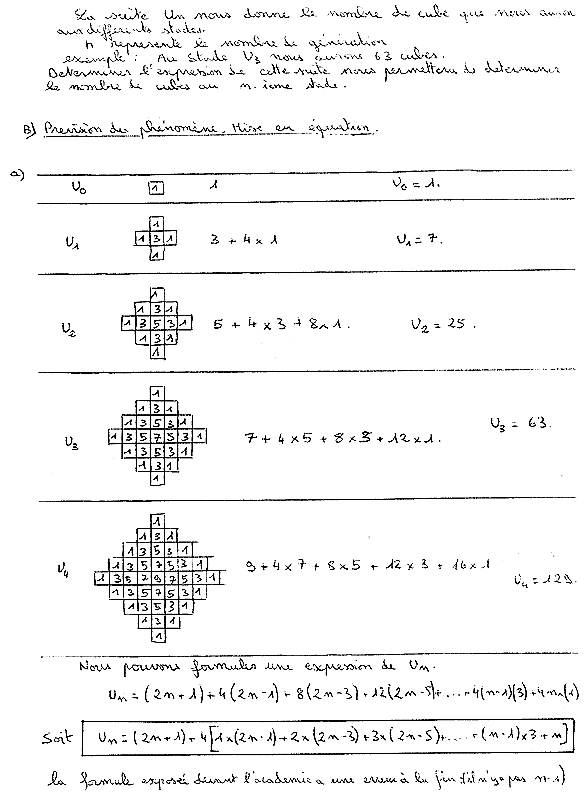
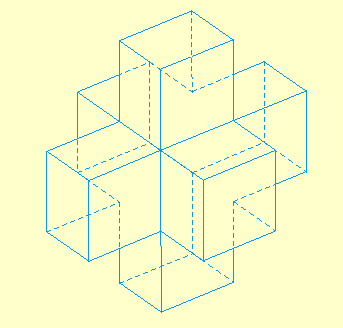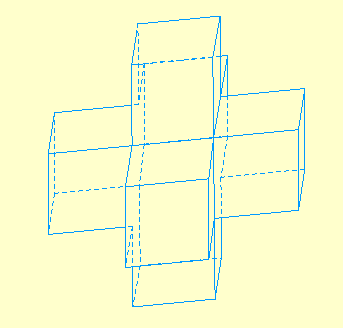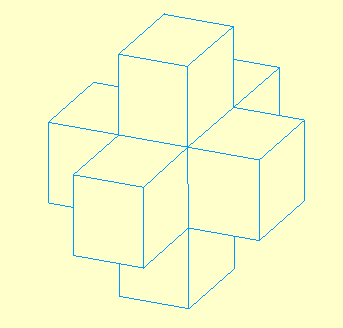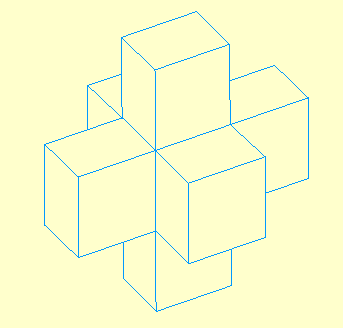
6 - Figures 3 D opaques en rotation
A l'occasion de la mise en ligne de cet ancien article d'abraCAdaBRI, le “webmestre” s'est amusé à aller un peu plus loin que la version papier … histoire d'alimenter les Alice-arguments : vous trouverez dans cette page la possibilité d'animer une rotation des générations 1 et 2 avec gestion des parties cachées.
Ces figures Cabri sont construites sur les mêmes principes que les animations de troncatures opaques disponibles à la Galerie d'Alice, avec la difficulté supplémentaire que le polyèdre à traiter n'est plus convexe.
La Génération 2
Traitement interactif de la perspective cavalière
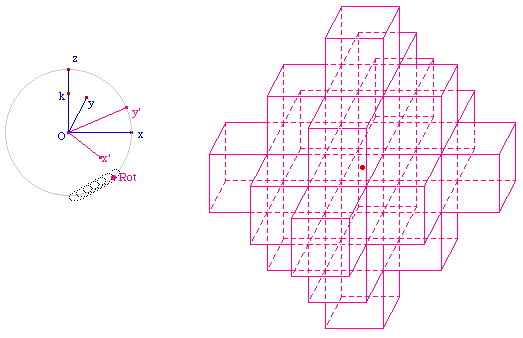
Lancer la figure Urbi2Op1.fig opaque
Variante solide
Elle consiste simplement en la suppression des arêtes en pointillé pour une version solide totalement opaque.
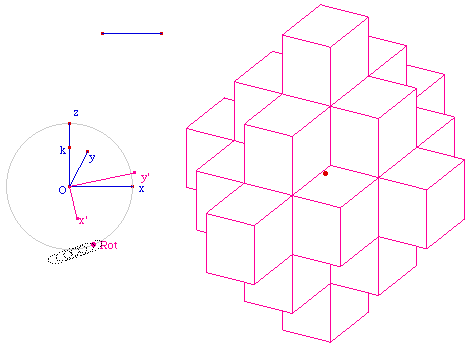
Lancer la figure Urbi2Op2.fig variante
Il est amusant aussi d'observer l'effet de trace sur ce mouvement de rotation en animation
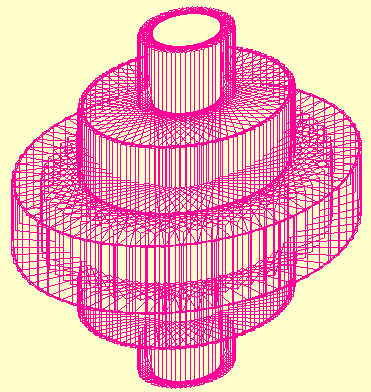
Pour illustrer une présentation (ou pour les accros qui veulent reprendre la figure)
Vous pouvez aussi charger un squelette de la construction :
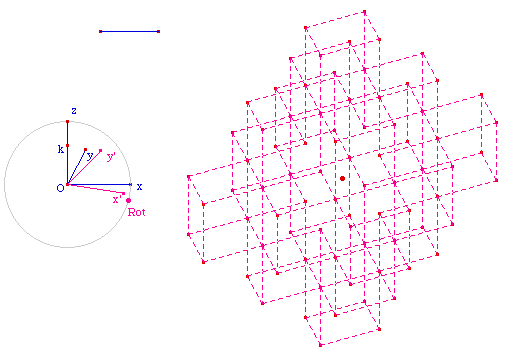
Lancer la figure Urbi2Squ.fig du squelette.
La Génération 1
Traitement interactif de la perspective cavalière
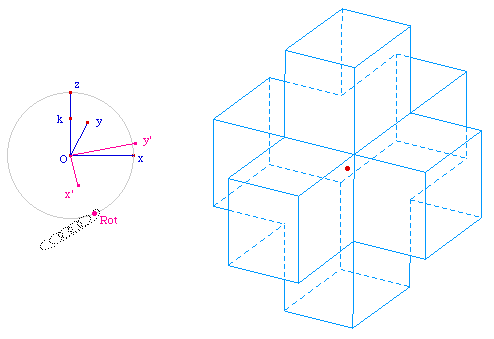
Lancer la figure Urbi1Op1.fig opaque
Voir une animation gif transparente de cette rotation
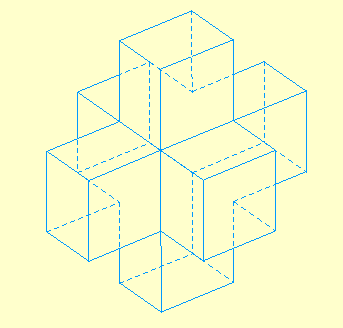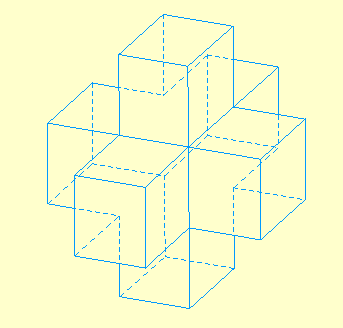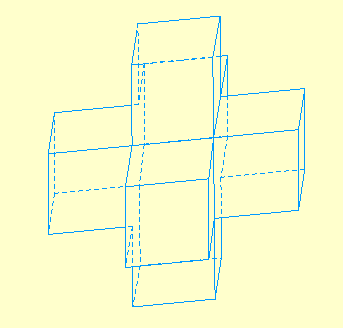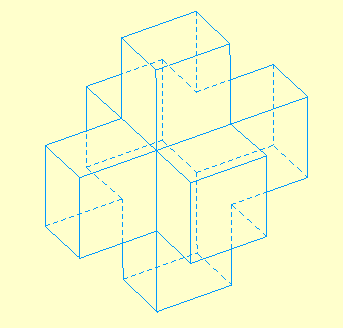
Variante solide
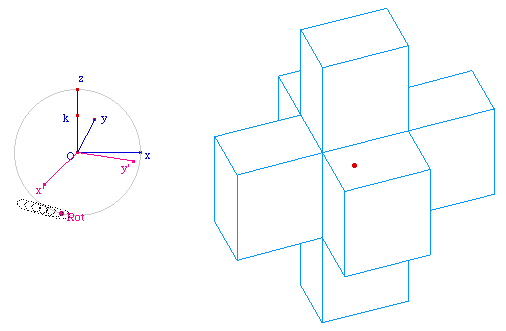
Lancer la figure Urbi1Op2.fig variante
Voir une animation gif opaque de cette rotation
Voir une animation gif transparente puis opaque de cette rotation