Een korte uitleg van "Le Mystère d'Urbicande"
(Professeur R. de Brok, Brüsel, ?)
Door dokter Jean-Paul Van Bendegem
Vertaald uit het Nederlands door Eilko Bronsema
De bijdrage van dokter Van Bendegem wordt kort vermeld in Le Guide des Cités, op pagina 126 van de oorspronkelijke uitgave. We zijn Olivier Tissot dank verschuldigd voor het speurwerk dat nodig was om hem op te sporen en de toestemming te krijgen om het volgende artikel te reproduceren.
Op pagina 19 van het bovengenoemde boek wordt een wiskundige formule gebruikt als argument tegen het bestaan van het Netwerk (Web). De formule van Robick,
Un = (2n+1) + 4(1(2n-1) + 2(2n-3) + … + n1)
is volgens de Brock wiskundig onjuist. De uitwerking van de rechterkant kan vervangen worden door de sommatie die de eenvoudige relatie van de Brok geeft:
Un = (2n+1)(2n2+2n+3)/3
Het commentaar van Eugen Robick zelf, genoteerd aan de zijkant van de pagina, zegt dat zijn formule het beeld van het Netwerk beter weergeeft. Dit kan alleen maar geïnterpreteerd worden als een verwijzing naar de piramidevorm - Robick bedoelde eigenlijk een octaëder (zie verder) - van het Netwerk. In deze korte tekst wil ik vier punten naar voren brengen:
- De juistheid van de gelijkheid van de formules van Robick en de Brok.
- De onjuiste weergave van de piramide op pagina 18 van het boek van de Brok.
- De deductie van de formule van Robick en zijn relatie tot de piramidevorm.
- De eenvoudige relatie tussen de formule van de Brok en de piramidevorm, die bewijst dat de formule van de Brok ook een getrouwe weergave van het fenomeen is.
(1) Laat ik beginnen met de formule van Robick:
Un = (2n+1) + 4(1(2n-1) + 2(2n-3) + … + n1)
De sommatie tussen de haakjes aan de rechterkant is het deel dat ons interesseert:
1.(2n-1) + 2.(2n-3)+ … + n.1
Het aantal termen in deze sommatie is n, als de sommatie tussen 1 en n ligt. Wat is de vorm van een algemene term voor deze ontwikkeling? Het is een product, waarvan de eerste factor een getal i is tussen 1 en n, dus 1 < = i < = n and the second factor is 2n - 2i + 1 . So the general term is:
i.(2n - 2i +1) (x)
Let me use ∑ to say that we need to make the summation of the terms like (x) where i is between i and n. Then we can make the formula of Robick a bit simpler:
Un = (2n+1) + 4 . ∑ i(2n - 2i + 1)
In deze laatste formule kunnen we i.(2n - 2i + 1) transformeren naar i.2n - 2i2 + i . Nu kunnen we de formule transformeren en vinden we:
∑ i.(2n - 2i + 1) = ∑ i.2n - ∑ 2i2 + ∑ i
De eerste term is ∑ i.2n . Omdat we in elke term 2n vinden kunnen we deze buiten het sommatieteken (∑) zetten: ∑ i.2n = 2n. ∑ i .
De derde term is ∑ i, dus we kunnen deze twee termen samenvoegen tot (2n+1). ∑ i . De waarde van ∑ i is een bekend wiskundig resultaat:
∑ i = n(n+1)/2
Het klassieke bewijs is als volgt:
∑ i = 1 + 2 +3 + … + n -1 + n
∑ i = n + n-1 + n-2 + … + 2 + 1
(het verwisselen van de termen verandert de sommatie niet).
Tel alles bij elkaar op:
2. ∑ i = (n+1) + (2+(n-1)+ … + ( (n-1)+2) + (n+1)
Aan de rechterkant staat n keer n+1, dus:
2. ∑ i = n(n+1) en dus i = n(n+1)/2
Dan blijft over ∑ 2.i2 term. Ook hier kunnen we de factor 2 vervangen, dus 2 . ∑ i2 . Ook deze keer vinden we een bekend resultaat:
∑ i2 = n(n+1)(2n+1)/6
Er zijn verschillende manieren om dat te bewijzen. i2 kan vervangen worden door i(i+1)-i, dus ∑ i2 = ∑ i(i+1) - ∑ i. De tweede term aan de rechterkant is al berekend, dus moeten we kijken naar i(i+1). Als we deze sommatie uitschrijven vinden we:
1 = 1(1+1)/2
1 2 = 2(2+1)/2
1 2 3 = 3(3+1)/2
…
1 2 3 … n = n(n+1)/2
Als we alles optellen vinden we:
n.1 + (n-2)2 + (n-3)3 + … + 1.n = ∑ i(i+1)/2
of ∑ i.(n-i+1) = ∑ i(i+1)/2
of 2. ∑ i.n - 2. ∑ i2 + 2.∑ i = ∑ i(i+1)
Als we ∑ i(i+1) in de bovenstaande formule vervangen, vinden we:
∑ i2 - 2. ∑ i.n - 2. ∑ i2 + 2. ∑ i - ∑ i
of 3. ∑ i2 = (2n+1) . ∑ i
met behulp van de laatste formule vinden we:
3 . ∑ i2 = (2n+1)n(n+1)/2
wat de formule geeft:
∑ i2 = n(n+1)(2n+1)/6
Wanneer we deze resultaten gebruiken, kunnen we de formule van Robick als volgt transformeren:
Un = (2n+1) + 4 .( (2n+1). ∑ i - i . ∑ i2)
Un = (2n+1) + 4. ( n(n+1)(2n+1)/2 - 2n(n+1)(2n+1)/6)
Un = (2n+1)(1 + 2.n(n+1) - 4.n(n+1)/3)
Un = (2n+1)(3 + 6.n(n+1) - 4.n(n+1)/3)
en tenslotte de formule van de Brok:
Un = (2n+1)(2n2+2n+3)/3
(2) De groei van de kubus volgt een heel eenvoudig patroon, zoals in wat volgt zal worden aangetoond, gebaseerd op het commentaar van de Brok. Als x staat voor één kubus van het netwerk, dan zal de volgende generatie van deze kubus uit 6 nieuwe kubussen bestaan (fig.1).
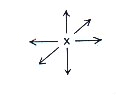
Als je begint met één kubus (de situatie U0) dan is de volgende generatie kubussen 1 + 6 = 7 = U1 kubussen. De lezer kan de volgende generaties zelf tekenen. Het ziet er ongeveer zo uit (fig.2).
 fig.2. het netwerk (web) |  fig.3. De Broks' onjuiste presentatie |
Dit komt niet overeen met de figuur op pagina 18 van het verhaal van De Brok. Deze figuur wordt gepresenteerd als fig. 3. Het feit dat de Brok zo'n meetkundige fout maakte, ondanks zijn ongelooflijke algebraïsche inzichten, past bij de theorie dat de Brok en Robick twee verschillende personen zijn. Het is niet onredelijk om te zeggen dat urbatect Robick in principe een geometrische kijk op de wereld heeft, en archivaris Isidore Louis heeft het mis als hij beweert dat beide personen dezelfde moeten zijn (zie L'Archiviste, stuk nr. 16).
(3) De deductie van de formule van Robick en zijn relatie tot de piramidevorm
De globale vorm van een piramide is als volgt (fig.4):

In lijn AB zal er in de nde generatie Un 2n+1 kubussen. Dan kijken we naar een kwart van de piramide (de vetgedrukte lijnen in figuur 4). Als we dit deel van bovenaf bekijken, zien we het volgende:
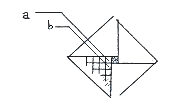
De kubus 'a' staat voor een kolom kubussen die er twee minder heeft dan de centrale kolom (één minder bovenaan en één minder onderaan), dus is het totaal aantal kubussen in deze kolom 1.(2n-1). De kubussen gemarkeerd met een 'b' hebben weer twee kubussen minder, dus is het totaal aantal 'b' kubussen 2.(2n-3). Als je zo doorgaat dan kom je uit op 'n' kubussen van n.1 . De totale som van dit kwart van de piramide is:
1.(2n-1)+2.(2n-3)+…+n.1
Het totaal aantal kubussen (in de nlaatste generatie) zal zijn:
Un = middenkolom + 4 keer de kwartieren of
Un = (2n+1)+ 4.(1.(2n-1)+2.(2n-3)+…+n.1)
of de formule van Robick.
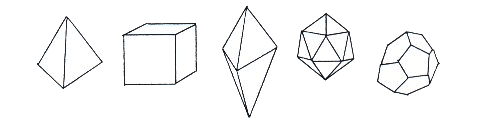
Deze formule benadrukt de bouw van een piramide, een octaëder om precies te zijn, als een constructie met een centrale kolom en vier eenvoudige symmetrische vormen rond deze kolom. Merk op dat dit niet de enige manier is om een piramide op een zuiver meetkundige manier te beschrijven. Het is zeer verrassend dat Robick niet heeft opgemerkt dat de piramide-octaëder een van de slechts vijf regelmatige Euclidische of Platonische vormen is (zie figuur 6). Het kan geen toeval zijn dat de piramide precies in het midden van hun progressieve schaal staat. Het is niet de eenvoudigste figuur, maar ook niet de meest complexe.
(4) De meetkundige interpretatie van de formule van de Brok.
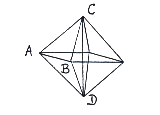
Kijk naar de octaëder (zie figuur 7). Elementaire wiskunde laat zien dat als de hoogte CD gelijk is aan H, dan is de zijde Z = AB gelijk aan √2. H/2.
Laten we terugkeren naar de formule van de Brok. Deze formule geeft het aantal kubussen weer. Als we de inhoud van deze kubuspiramide willen weten, moeten we deze hoeveelheid vermenigvuldigen met de inhoud van een kubus, α3</supp>waarbij α de lengte van een zijde van de kubus is. De inhoud van de piramide is dus: I = (2n+1)(2n<sup>2+2n+3)α3/3 (xx)
De hoogte van de piramide is 2n+1 kubussen. Als H gelijk is aan (2n+1).α, met andere woorden H is de hoogte gemeten in afstand: H = (2n+1).α.
De formule (xx) kan als volgt herschreven worden:
I = ( (2n+1).α.( (√2(n+1/2α))2 + 5.α2/2)/3
In deze formule kunnen we (2n+1).α vervangen door H en (n+1/2).α door H/2 en √2.H/2 door Z:
I = H.(Z2+5.α2/2)/3
Als we een zeer groot aantal kubussen schatten voor een gegeven hoogte H (om op deze manier een “klassieke” piramide-octagon te krijgen), dan zal het aantal kubussen erg klein worden, dus in bovenstaande formule kunnen we het 5,2/2 deel overslaan en de formule voor de inhoud houden:
I = H.Z2/3
Dit is precies de formule voor de inhoud van een octaëder!
Dit betekent dat de formule van de Brock een discrete weergave is van de formule voor de inhoud van een octaëder, waarbij de factor (2n+1) staat voor de hoogte en (2n2+2n+3) staat voor de oppervlakte van het vierkant waarop de octaëder is gebouwd. Het kan dus moeilijk worden ontkend dat de formule van de Brok, net als de formule van Robick, het essentiële deel van het netwerk (web) bevat.
Een laatste kleine opmerking: meer steun voor het niet-algebraïsche maar geometrische inzicht van Eugen Robick kan worden gevonden in zijn commentaar. Hij schrijft “ma formule, en son expansion infinie,…” (pagina 19). Robick's formule bevat een ontwikkeling, maar voor elke generatie Un zal deze eindig zijn.







