Une brève explication du "Mystère d'Urbicande"

(Professeur R. de Brok, Brüsel, ?)

Par le Docteur Jean-Paul Van Bendegem
Traduit du néerlandais par Eilko Bronsema

La contribution du Docteur Van Bendegem est brièvement mentionnée dans Le Guide des Cités, à la page 126 de l'édition originale. Nous sommes redevables à Olivier Tissot du travail de détective qui nous a permis de retrouver sa trace et d'obtenir l'autorisation de reproduire l'article suivant.

A la page 19 du livre mentionné ci-dessus, une formule mathématique est utilisée comme argument contre l'existence du Réseau (Web). La formule de Robick,

U_n = (2n+1) + 4(1(2n-1) + 2(2n-3) + … + n1)

est, selon de Brock, mathématiquement incorrecte. Le développement du côté droit peut être remplacé par la sommation qui donne la simple relation de de Brok:

U_n = (2n+1)(2n²+2n+3)/3

Le commentaire d'Eugen Robick lui-même, noté sur le côté de la page, indique que sa formule représente mieux l'image du réseau. Cela ne peut être interprété que comme une référence à la forme pyramidale - Robick voulait en fait parler d'un octaèdre (voir plus loin) - du Réseau. Dans ce court texte, je voudrais exprimer quatre points :

L'exactitude de l'égalité des formules de Robick et de de Brok.
La représentation incorrecte de la pyramide à la page 18 du livre de de Brok.
La déduction de la formule de Robick et sa relation avec la forme de la pyramide.
La relation simple entre la formule de de Brok et la forme de la pyramide, qui prouve que la formule de de Brok est aussi une représentation fidèle du phénomène.

(1) Commençons par la formule de Robick :

U_n = (2n+1) + 4(1(2n-1) + 2(2n-3) + … + n1)

La somme entre les crochets du côté droit est la partie qui nous intéresse :

1.(2n-1) + 2.(2n-3)+ … + n.1

Le nombre de termes de cette somme est n, si la somme est comprise entre 1 et n. Quelle est la forme d'un terme général pour ce développement ? Il s'agit d'un produit dont le premier facteur est un nombre i compris entre 1 et n, donc 1 < = i < = n and the second factor is 2n - 2i + 1 . So the general term is:

i.(2n - 2i +1) (x)

Let me use ∑ to say that we need to make the summation of the terms like (x) where i is between i and n. Then we can make the formula of Robick a bit simpler:

U_n = (2n+1) + 4 . ∑ i(2n - 2i + 1)

Dans cette dernière formule, nous pouvons transformer i.(2n - 2i + 1) en i.2n - 2i2 + i . Maintenant, nous pouvons transformer la formule et nous trouverons :

∑ i.(2n - 2i + 1) = ∑ i.2n - ∑ 2i² + ∑ i

Le premier terme est ∑ i.2n . Comme nous trouvons 2n dans chaque terme, nous pouvons le placer à l'extérieur du signe de sommation (∑) : ∑ i.2n = 2n. ∑ i .

Le troisième terme est ∑ i, nous pouvons donc joindre ces deux termes à (2n+1). ∑ i . La valeur de ∑ i est un résultat mathématique connu:

∑ i = n(n+1)/2

La preuve classique est la suivante :

∑ i = 1 + 2 +3 + … + n -1 + n
∑ i = n + n-1 + n-2 + … + 2 + 1

(l'inversion des termes ne modifie pas la somme).

Additionnez tout :

2. ∑ i = (n+1) + (2+(n-1)+ … + ¹⁾² + 5.α²/2)/3

Dans cette formule, on peut remplacer (2n+1).α par H et (n+1/2).α par H/2 et √2.H/2 par Z :

I = H.(Z²+5.α²/2)/3

Lorsque nous estimons un très grand nombre de cubes pour une hauteur H donnée (pour obtenir de cette manière une pyramide octogonale “classique”), alors deviendra très petit, donc dans la formule ci-dessus nous pouvons sauter la partie 5.2/2 et garder comme la formule pour le contenu :

I = H.Z²/3

C'est exactement la formule pour le contenu d'un octaèdre!

Cela signifie que la formule de Brock est une représentation discrète de la formule du contenu d'un octaèdre, où le facteur (2n+1) représente la hauteur et (2n²+2n+3) mesure l'aire du carré sur lequel l'octaèdre est construit. On peut donc difficilement nier que la formule de de Brok, comme celle de Robick, contient l'essentiel du réseau (web).

Un dernier petit commentaire : la vision non algébrique mais géométrique d'Eugen Robick est étayée par son commentaire. Il écrit “ma formule, en son expansion infinie,…” (page 19). La formule de Robick contient un développement, mais pour chaque génération U_n elle sera finie.

¹⁾

n-1)+2) + (n+1) Le côté droit est n fois n+1, donc : 2. ∑ i = n(n+1) en so i = n(n+1)/2 Cela nous laisse avec le ∑ 2.i² . Là encore, nous pouvons remplacer le facteur 2, donc 2 . ∑ i² . Cette fois encore, nous trouvons un résultat connu : ∑ i² = n(n+1)(2n+1)/6 Il y a plusieurs façons de le prouver. i² peut être remplacé par i(i+1)-i, donc ∑ i² = ∑ i(i+1) - ∑ i. Le deuxième terme du côté droit a déjà été calculé, nous devons donc nous intéresser à i(i+1). Si nous écrivons cette sommation, nous trouverons : 1 = 1(1+1)/2
1 2 = 2(2+1)/2
1 2 3 = 3(3+1)/2
…
1 2 3 … n = n(n+1)/2
En faisant la somme de tous les éléments, on obtient n.1 + (n-2)2 + (n-3)3 + .. + 1.n = ∑ i(i+1)/2 ou ∑ i.(n-i+1) = ∑ i(i+1)/2 ou 2. ∑ i.n - 2. ∑ i² + 2.∑ i = ∑ i(i+1) En remplaçant ∑ i(i+1) dans la formule ci-dessus, on trouve : ∑ i² - 2. ∑ i.n - 2. ∑ i² + 2. ∑ i - ∑ i ou 3. ∑ i² = (2n+1) . ∑ i à l'aide de la dernière formule on trouve 3 . ∑ i² = (2n+1)n(n+1)/2 ce qui donne la formule : ∑ i² = n(n+1)(2n+1)/6 En utilisant ces résultats, nous pouvons transformer la formule de Robick comme suit : U_n = (2n+1) + 4 .( (2n+1). ∑ i - i . ∑ i2)
U_n = (2n+1) + 4 ( n(n+1)(2n+1)/2 - 2n(n+1)(2n+1)/6)
U_n = (2n+1)(1 + 2.n(n+1) - 4.n(n+1)/3)
U_n = (2n+1)(3 + 6.n(n+1) - 4.n(n+1)/3)
et enfin la formule de de Brok: U_n = (2n+1)(2n²+2n+3)/3

(2) La croissance du cube suit un schéma très simple, comme cela sera démontré dans ce qui suit, sur la base des commentaires de de Brok. Si x représente un cube du réseau, la prochaine génération de ce cube sera composée de 6 nouveaux cubes (fig.1).

fig.1 schéma de croissance

Si vous commencez avec un cube (la situation U₀), la génération suivante de cubes sera 1 + 6 = 7 = U₁ cubes. Le lecteur peut dessiner lui-même les générations suivantes. Cela ressemblera à quelque chose comme ceci (fig.2).

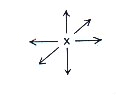
fig.2. le réseau (web)

fig.3. Présentation incorrecte de De Broks

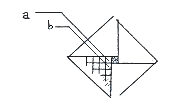
Cela ne correspond pas à la figure présentée à la page 18 de l'article de De Brok. Cette figure est présentée comme la fig. 3. Le fait que de Brok ait commis une telle erreur géométrique, en dépit de ses incroyables connaissances algébriques, conforte la théorie selon laquelle de Brok et Robick sont deux personnes différentes. Il n'est pas déraisonnable de dire que l'architecte Robick a essentiellement une vision géométrique du monde, et l'archiviste Isidore Louis a tort lorsqu'il prétend que les deux personnes doivent être les mêmes (voir L'Archiviste, pièce n° 16).

(3) La déduction de la formule de Robick et sa relation avec la forme de la pyramide La forme globale d'une pyramide est la suivante (fig.4) :

Fig.4. Forme de la pyramide

Dans la ligne AB, il y aura dans la n^génération génération U_n 2n+1 cubes. Nous examinons ensuite un quart de la pyramide (les lignes en gras dans la figure 4). Lorsque nous regardons cette partie depuis le haut, nous voyons ceci :

Fig.5. vue du dessus

Le cube 'a' représente une colonne de cubes qui a deux cubes de moins que la colonne centrale (un de moins en haut et un de moins en bas), ce qui fait que le nombre total de cubes dans cette colonne est de 1.(2n-1). Les cubes marqués d'un 'b' ont à nouveau deux cubes de moins, de sorte que le nombre total de cubes 'b' est de 2.(2n-3). Si vous continuez ainsi, vous obtiendrez 'n' cubes de n.1. La somme totale de ce quart de la pyramide est : 1.(2n-1)+2.(2n-3)+…+n.1 Le nombre total de cubes (dans le n^e génération) sera : U_n = colonne centrale + 4 fois les quarts ou U_n = (2n+1)+ 4.(1.(2n-1)+2.(2n-3)+…+n.1) ou la formule de Robick. Cette formule met l'accent sur la construction d'une pyramide, un octaèdre pour être plus précis, comme une construction avec une colonne centrale et quatre formes symétriques simples autour de cette colonne. Notez que ce n'est pas la seule façon de décrire une pyramide d'une manière purement géométrique. Il est très surprenant que Robick n'ait pas remarqué que la pyramide-octaèdre est l'une des cinq formes régulières euclidiennes ou platoniciennes (voir figure 6). Ce n'est pas une coïncidence si la pyramide se trouve exactement au milieu de leur échelle progressive. Ce n'est pas la figure la plus simple, mais ce n'est pas non plus la plus complexe.

Fig. 6. Les cinq formes platoniciennes

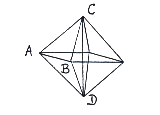
(4) L'interprétation géométrique de la formule de Brok. Observez l'octaèdre (voir figure 7). Les mathématiques élémentaires montrent que si la hauteur CD est égale à H, alors le côté Z = AB est égal à √2. H/2.

Fig.7. l'octogone

Revenons à la formule de de Brok. Cette formule indique le nombre de cubes. Si nous voulons connaître le contenu de cette pyramide cubique, nous devons multiplier ce montant par le contenu d'un cube, α^{3</supp>où α est la longueur d'un côté du cube. Le contenu de la pyramide est donc :
I = (2n+1)(2n<sup>2}+2n+3)α³/3 (xx) La hauteur de la pyramide est de 2n+1 cubes. Si H est égal à (2n+1).α, autrement dit H est la hauteur mesurée en distance : H = (2n+1).α. La formule (xx) peut être réécrite comme suit : I = ( (2n+1).α.( (√2(n+1/2α